村上飛鳥ASK どうもこんにちは、エイメイ学院のASKです✋️
先週12月20日に行った合格講座のランキングを発表いたします👑
この日から、実際の埼玉県公立入試の過去問をやってもらっていますが
その結果がどうだったのか？！
御覧ください✋️
はい、いかがでしょうか
埼玉県の平均点が43.2点なのに対して54.2点と大きく上回っておりますね✨️
ここで一つのデータを見ていただきましょう
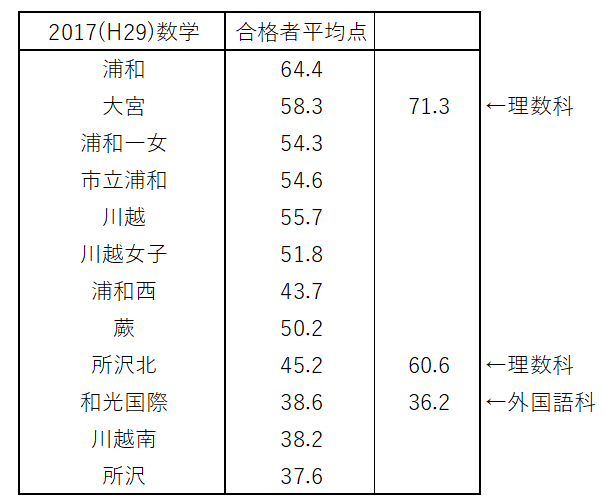
こちらは当時の受験生たちの合格者平均点になります
平均点54.2点というのがどれだけ凄いか分かりますね笑
御三家の浦和一女や、市立浦和に匹敵しています
今回の年度は、学校選択問題が初めて行われた年度ですので
当時は、難易度に対応できなかった受験生もいたかと思います
その中で、EIMEIグループの生徒たち、素晴らしい結果を出してきていますね～✨️
今後に期待！
当時は公式の証明が出ていた！今後は？！
さて、今回の学校選択問題では
解の公式の証明が出題されていました
同様に、この翌年も、とある公式の証明問題が出題されています
当時は話題になりましたよ～
まさか解の公式の証明が出るとは
しかも、正答率は2.4%と極めて低い
受験生の意表を突く問題だったのがよく分かります笑
そこからですかね、定期テストにも証明問題が出るようになり
学校の授業でも、公式の証明を丁寧にやっているなと感じるようになったのは
当然、EIMEIの授業でも、公式の証明をやりました
こうやって入試問題というのは、年々進化していくものなんです
そして、塾や学校によって対策されていきます笑
２～３年くらいしたら、公式の証明そのものは出題されていません
今後も、出る可能性は、ゼロではありませんが
少なくとも同じものが出題される可能性は低いでしょう
じゃあ公式の証明はやらなくていいのか？
いいえ、公式の証明は、根本への理解に繋がります
例えば解の公式の証明の中には、たくさんの大事な要素が詰まっています
・等式の性質の運用
・平方根の性質の理解
・因数分解による平方完成
・文字を文字のまま処理していくこと
解の公式の証明をただ暗記するのではなく
要素に分解したときの大事な部分に、しっかり目を向けておきましょう
図形も然りです
・平行線と線分の比
・中点連結定理
・角の二等分線定理
・円周角の定理
・内接四角形の定理
・三平方の定理
などなど
これらの証明、全部できますか？
その証明を理解することで、図形そのものに対する見方が広がります
一度通しで良いので、やっておくことを非常にオススメいたしますよ
年末年始、時間があるときがチャンスです
ぜひ、教科書を手にとってやってみてくださいね👍️
PR：アナザーverの缶バッジ渡していっています～✨️
